0 引言

    在實時圖像處理、數字信號處理等領域內，經常需要對非線性函數進行高速計算^[1]。而在人工神經網絡中更是需要對大量的非線性函數進行計算。因此，在人工神經網絡的研究領域內，研究如何高速地處理非線性函數具有十分重要的意義。在人工神經網絡中應用最為廣泛的是Sigmoid函數。目前對于Sigmoid函數實現技術的研究主要分為軟件實現和硬件實現兩個方面。由于軟件相比硬件而言速度較慢并且并行程度很低，所以無法滿足其快速處理的要求^[2]。因此，在超大規模集成電路快速發展的當今時期，研究如何利用硬件快速處理Sigmoid函數顯然更加有意義。

    FPGA憑借其可重構技術的靈活性，成為解決Sigmoid函數高速計算問題的有力工具。目前利用FPGA計算Sigmoid函數常用的方法有查找表法、CORDIC算法、Taylor級數展開法和分段線性逼近法。查找表法^[3]提前將所有的計算結果保存在一個ROM中，這種方法計算方便且容易實現，但是隨著函數計算精度的提高和擬合區間的增加，其所需求的存儲資源會顯著增加，資源消耗很高。CORDIC算法^[4]通過多次迭代將一些復雜的運算轉換成為簡單的運算，但是隨著精度增高，其算法的迭代次數也會提高，計算速度會減慢。Taylor級數展開法^[5]在精度要求較高的條件下會增加乘法器和加法器的使用，資源消耗巨大。分段線性逼近法^[6-7]將查找表和低階多項式相結合，計算速度較快，是當前解決此問題的主流方法，然而在有限的分段區間用低階的多項式進行擬合運算，其計算結果在精度上并沒有優勢，難以實現高精度的運算要求。

    為了解決上述問題，本文采用傳統的分段非線性逼近法來處理Sigmoid函數。文獻[8]中使用了分段非線性逼近法來處理神經網絡中常見的雙曲正切函數，然而文中并沒有給出分段方法的依據，同時在各小段的分段區間所得到的精度也差異很大。因此，本文針對這一問題，以Sigmoid函數為研究對象，結合Sigmoid函數自身對稱及其導數不均勻的性質，利用數值分析中的最小二乘法作為逼近原理，給出合理的分段方式。同時給出對比均勻分段的處理方式下逼近精度的差異情況。利用硬件描述語言實現硬件結構的設計，并在Xilinx Virtex-5系列的XC5VLX110T器件上完成實際驗證和性能測試，從資源使用、運算速度同計算精度等方面對設計結果進行合理評估。

1 Sigmoid函數的分段非線性擬合方案及結果分析

    分段非線性逼近法的基本原理是用高階多項式來逼近曲線。首先將待逼近函數按照一定的方式進行分段，之后對每一個小段構建高階多項式近似地代替原曲線，從而將復雜的非線性函數的計算問題轉換成為多項式的計算問題。

    由泰勒公式的原理可知，函數在某一點按照泰勒公式展開，隨著展開的項數越來越多，逼近式的誤差會越來越小。并且，隨著項數的增加，每一項在數值上逐漸遞減，并最終趨向于無窮小。函數在某一點按照泰勒公式展開，保留N階多項式時，其之后的所有項數均影響誤差，并且(N+1)階導函數的數值直接影響N階多項式的逼近結果。具體影響的方式為：N+1階導數取絕對值后，其值越大，表明函數在這一點處使用N階多項式逼近的誤差越高，因此在這點處對應的分段區間間隔應該相對較小；其值越小，表明函數在這一點處使用N階多項式逼近的誤差越低，因此在這點處對應的分段區間間隔應該相對較大。在考慮分段時，可以根據N+1階導數的數值大小，將函數的分段區間進行動態調整，避免造成誤差過大。通過這樣的處理方式，可以對分段方式進行一些優化。下面結合Sigmoid函數進行具體分析。

    首先分析Sigmoid函數及其導函數的性質，如圖1。F(x)為Sigmoid函數，G(x)為其4階導函數。在保證足夠的分段區間時，使用3階多項式就能夠得到較高的逼近精度。因此，本文使用3階多項式逼近Sigmoid函數，4階導函數G(x)直接影響逼近的誤差。通過研究圖像，得出以下結論：

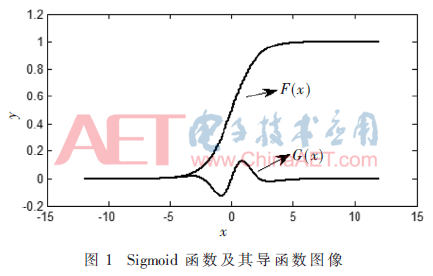
    (1)Sigmoid函數F(x)是以點(0，0.5)為對稱中心的函數，因此在計算Sigmoid函數值時只需計算正區間或負區間，另一半可通過對稱關系得到；

    (2)以正區間為研究對象，Sigmoid函數的4階導數在x=1處附近取得最大值，并向兩側衰減，隨著x的不斷增大，4階導數最終趨向于0。

    為了驗證這種基于導數的分段方法在逼近結果的精度方面是否具有優勢，本文選擇了將這種分段方式與傳統的等間距分段方式作對比。首先，將Sigmoid函數的待處理區間進行等分，之后比較每個子區間的函數4階導數的整體變化規律，對導數相對較大的區間進行縮短，對導數相對較小的區間進行擴展。分別對這兩種分段方式下所有的子區間構建3階多項式，通過對比函數各子區間及整體區間的誤差情況來驗證此分段方法的優勢。

    本文選用MATLAB作為函數擬合工具，構建擬合多項式使用最小二乘法原理，數據類型選取雙精度浮點數，這樣可以保證在計算過程中精度比較高。下面分別給出兩種分段方式下的分段結果及誤差對比。為了保證實驗結果可靠，各分段區間取的數足夠大(這里以0.000 1為間隔取數)，結果見表1。

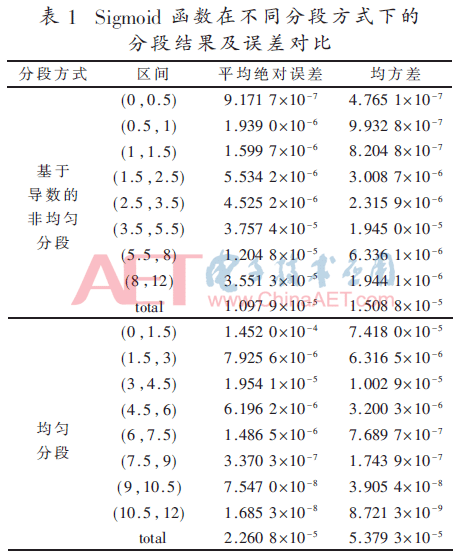
    通過表1可以得出，當使用三階多項式對Sigmoid函數進行逼近時，參照4階導函數的數值而分段的處理方式在平均絕對誤差和均方差兩項指標上均優于等間距分段的處理方式。從整體區間上看，平均絕對誤差減小了51.4%，均方差減小了71.9%。

2 Sigmoid函數的FPGA實現

    為了實現高精度的擬合要求，本文采用表1中基于導數的分段方式，使用三階多項式對Sigmoid函數進行擬合處理，并給出其FPGA實現結構，如圖2所示。設三階多項式為y=Ax³+Bx²+Cx+D，其在FPGA中的計算流程為：

    (1)取系數。各分段區間下的系數A、B、C、D預先存儲在RAM中，通過輸入x取出與之對應的系數A、B、C、D。

    (2)計算Cx和x²。

    (3)計算Cx+D、Bx²和x²。

    (4)計算Bx²+Cx+D和Ax³。

    (5)計算Ax³+Bx²+Cx+D。

    (6)用1和步驟(5)的結果做減法。

    (7)選擇器。當輸入的x為非負數時，輸出為步驟(5)的結果；若輸入的x為負數，輸出為步驟(6)的結果。

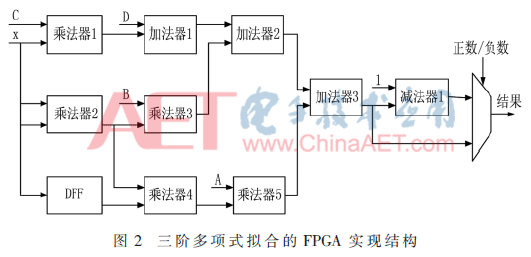
    上述所有的乘法器、加法器和減法器的設計采用Xilinx公司提供的32位單精度浮點型IP核實現，整個算法采用了流水線結構，數據輸入后，10個周期延遲后得到計算結果。具體實驗數據如表2所示。

    在實驗過程中，表1的誤差結果是由算法在FPGA上計算得到的結果與Sigmoid函數的真實值(精度遠高于實驗的精度)之間的對比求得的。表2中的誤差結果與表1中的誤差結果相比較在平均絕對誤差方面略有不足，是由于在FPGA中使用的32位單精度浮點數在精度上不同與MATLAB上使用的64位雙精度浮點數，所以兩者之間存在略微差別，然而并不影響算法的準確性。

    采用基于導數的分段方式并使用三階多項式的擬合方案在FPGA上所使用的資源雖然比經典的CORDIC算法及分段線性逼近方法較多，然而這種擬合方案在算法的精度上達到了10^-5數量級，各小段分段區間甚至達到10^-6數量級。當然，采用更高階數的多項式逼近在理論上能夠實現更高的精度，然而這樣的代價是會消耗更多的硬件資源。本文使用的分段非線性逼近法對Sigmoid函數的處理結果上，精度遠遠大于另兩種算法在現有的文獻中所取得的精度。并且若要達到較高精度，CORDIC算法會大大的增加迭代次數從而降低運算速度，分段線性逼近則會大大的增加存儲資源。

3 結論

    本文針對人工神經網絡中應用最為廣泛的Sigmoid函數，采用傳統的分段非線性逼近方法，結合Sigmoid函數自身對稱的性質及其導數不均勻的特點，給出合理的分段方式，在各小段分段區間內使用數值分析中經典的最小二乘法作為擬合逼近原理，得出初始分段間距同逼近多項式的階數對擬合結果精度的影響。按照上述方法給出一種在精度上達到了10^-5數量級的Sigmoid函數的擬合方案，實現了現階段對Sigmoid函數的高速、高精度的處理要求。

參考文獻

[1] JAIN V K，LIN L.High-speed double precision computation of nonlinear functions[C]//Symposium on Computer Arithmetic.IEEE Computer Society，1995：107.

[2] MOLZ R F，ENGEL P M，MORAES F G，et al.Codesign of fully parallel neural network for a classification problem[J].

[3] LEBOEUF K，NAMIN A H，MUSCEDERE R，et al.High speed VLSI implementation of the hyperbolic tangent sigmoid function[C]//International Conference on Convergence and Hybrid Information Technology.IEEE，2008：1070-1073.

[4] 萬書芹，陳宛峰，黃嵩人，等.基于改進CORDIC算法實現高速直接數字頻率合成器[J].儀器儀表學報，2010，31(11)：2586-2591.

[5] OUALI J，SAUCIER G.Fast generation of neuro-ASICs[M]//International Neural Network Conference.1990.

[6] ARMATO A，FANUCCI L，SCILINGO E P，et al.Low-error digital hardware implementation of artificial neuron activation functions and their derivative[J].Microprocessors & Microsystems，2011，35(6)：557-567.

[7] BASTERRETXEA K，TARELA J M，DEL CAMPO I.Digital design of Sigmoid approximator for artificial neural networks[J].Electronics Letters，2002，38(1)：35-37.

[8] XIE Z Z，ZHANG S Y.A non-linear approximation of the sigmoid function based FPGA[M]//Proceedings of the 2011，International Conference on Informatics，Cybernetics，and Computer Engineering(ICCE2011) November 19-20，2011，Melbourne，Australia.Springer Berlin Heidelberg，2011：221-223.

作者信息：

宋宇鯤，高曉航，張多利，杜高明

(合肥工業大學 微電子設計研究所，安徽 合肥230009）